|
1st Stage:Scene 4 |
探し求めた記数法
というのは、すべての結論には理由とプロセスがあり、それを「納得した上で理解しなければ身につかない!」と老師自身が体験してきたからだった。同時に、このテーマにはそれだけの重要性があるということでもあろう。
まず、なぜデジタルの世界そのものである2進法に対し、あえて「相性のよい記数法を求めようとしているのか?」という疑問がある。そんなことをしなくても、2進法のままで構わないはずだし、逆にそのほうがよいのでは……とも思えるからだ。
実は、2進法の最大の悩みは桁数の多さにある。すでに図1-3.2によって、2進法で4桁を使っても、10進法の0〜15までしか表せないことがわかっている。もちろん、桁数が多くてもコンピュータのほうは一向に困らないのだが、それをコントロールするわれわれ人間のほうがまいってしまうのだ。
「どうして人間はまいってしまうんスか?」
「10進数でも同じことじゃよ。10桁、20桁……と桁数が増えれば、それだけ数を間違える確率も高くなるじゃろ」
「フム、確かにそのとおりッス」
「ましてや、1と0の羅列が続けばミスをすることは火を見るより明らかじゃ。それなのに、そのミスを発見するのは至難のわざ……」
「そんなに難しいことッスか?」
とりあえず、1バイト(8ビット)ではどんな状況になるのか、相性のよい記数法を探すためにもジックリと見てもらいたい。

省略部分のある不完全な表だが、1バイトで10進法の0〜255が表現できることが読み取れる。
これは、下位4ビットが16通り(0〜15)なら、上位4ビットも同じく16通りの表現ができるわけで、16×16=256通り(0〜255)となることは、計算上からも容易に想像がつくだろう。
問題なのは、例えば10進法で22と25は即座に違いがわかるのに、00010110と00011001となると瞬時の判別が困難ということ。さらに、それが連続すればどうなるか。ミスの発生が当然なら、それを発見しにくいのも当然のことといえよう。
だからこそ、記数法を変えて「数値として人間に扱いやすくする」わけである。そのためには、2進法との換算がスッキリしていなければならない。ここに、相性のよさを求める理由がある。
そこで、マカイ老師のヒントにもあった2進数における桁上がりの位置が重要なポイントとなる。本表では▲印が付けられているので一目瞭然だ。
成康は、下位4ビットだけを見て4進法か8進法が好相性と推理したが、0〜3までしか使わない4進法は、肝心の桁数が半分になるだけ。これでは、10進法と比較しても桁数の面で魅力に欠ける。
「ということは、正解は8進法ッスね!」
「マァ、待て。あわてるでないぞ。コンピュータには、もう1つ数学的に忘れてはならない要素があるんじゃ」
「なんスか、その要素って?」
「それはじゃ、前回も示したように8ビット、つまり1バイトが重要な単位となっているということ。これを無視して好相性とはなり得ないのじゃよ!」
「じゃ……8進法は?」
「ベストではないということじゃ!」
0〜7を使う8進法は、3ビット単位で桁上がりを起こす。このことは、2進法との相性ではなく8ビットに対する割り切れなさが問題となるのだ。
|
8進法 ここではバイトとの相性から不適としたが、過去においては8進法が採用されたこともある。 そうした経緯から、現在でも完全否定されているわけではないが、パソコンにおいては「実需もメリットもない!」のが現状である。 |
これは1バイト(8ビット)を上位/下位4ビットに分けて変換することができ、記数法変換のシステムが非常にわかりやすい。つまり、4ビットを1桁にまとめるだけで16進数への変換が完了してしまうのである。
「そうはいっても、16進法っていったら12進法のダースより大きい記数法でしょ!」
「そのとおりじゃよ」
「あれって反面教師じゃなかったの。また、同じような算数の問題になるんじゃ、ほんとにシャレになんないッスよ! 」
「これこれ、いつからセッカチ屋になったんじゃ。コンピュータにおける16進法は、キチンと1桁で0〜15を表現できるように考えられておる」
「エッ、どうやって……?」
「これが、その証拠じゃ!」
不安がる成康にマカイ老師が示した証拠とは、机の上に並べた16個のリンゴだった。そこには、ダースとは明らかに違う独立した16進法の姿があった。
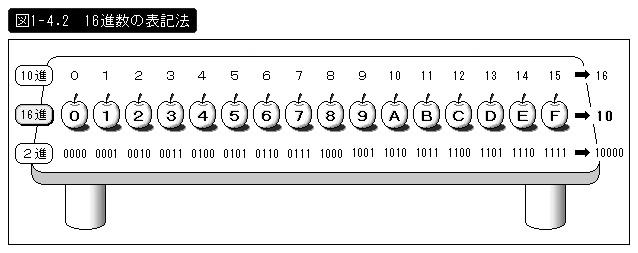
なんと、16進数の9の次にはA〜Fとアルファベットが続き、17個目へ桁上がりをするときに10になっている。
これならば、2進数と16進数の変換がシンプルというのも納得がいくだろう。この図を見れば、手計算をすることなく4ビット単位で相互に変換が可能になるのだ。
例えば、16進数の9Aを2進数にしたければ、9の1001とAの1010をそのまま並べればよいのだ(9A=10011010)。もちろん、その逆も同様に単純だ。この手軽さこそが、探し求めた好相性だったのである
参考までに、2進数から10進数への変換は、ビットごとに≪2の桁乗≫を掛けて求めるので、非常に面倒なものになる。逆に、10進数から2進数への変換は、2で割り算ができなくなるまで行い、その都度の剰余がビット0からの値となる。

いずれも「見るのもイヤ!」なほどの面倒さだ。もちろん、関数電卓を利用すれば一発で完了するが、ここでは「それをやっちゃァ、おしまいヨ!」である。両者の相性の悪さを身をもって知ることが、とりもなおさずここでの目的なのだから……。
|
こう書くと、何のために16進法を探し求めたのかと責められそうだが、実はデジタルの世界においても使い慣れた10進法と完全決別しているわけではない。その根拠や細かい用途はともかく、2のn乗値を覚えておくと何かと便利なのだ。
イチロク(16)とイチニッパ(128)でイチヨンヨン(144)。ニゴロ(256)とゴイチニ(512)でチィロンパ(768)というように、コンピュータに関する数値には麻雀の世界と妙に近いものがある。 実際、パソコンのカタログなどにある内部仕様書を見ると、こうした数字がたくさん並んでいるのだ。さすが、中国三千年の歴史はダテじゃない!? |